
What is Linear Motion?
Linear motion, also known as rectilinear motion, refers to the movement of an object along a straight line, where the position of the object changes over time (t). It can be broken down into two types: uniform linear motion, where the object moves at a constant velocity with zero acceleration, and non-uniform linear motion, where the object experiences a variable velocity and non-zero acceleration. A simple example is a 100-meter dash, where an athlete runs in a straight line along a track, moving through space, with velocity changing over time due to various factors like external forces.
This type of motion is crucial in understanding basic principles like Newton’s first law of motion, which states that an object in motion will continue moving in a straight line unless acted upon by an external net force. For instance, gravity and friction can influence the direction and speed of the object, causing it to deviate from its linear motion. In such cases, the directional components of the vectors are not constant, and this requires a more simplified analysis to understand the forces at play. Linear motion helps define a system where objects move in one-dimensional motion along a specified axis without changing their direction.
Displacement in Linear Motion
Displacement refers to the shortest distance between an object’s initial position (x1) and its final position (x2). In linear motion, displacement is a straight line in a single dimension, and it is different from the distance traveled, which is the total length the object moves. For example, if a person travels to work and returns home, their displacement is zero because they end up at their starting point, even though the distance traveled is not zero.
In rotational motion, we have angular displacement (θ), measured in radians, which is similar to displacement but for circular paths. The SI unit of displacement is the meter, and we can calculate it using the formula:
Δx = x₂ – x₁
Displacement gives a clearer picture of an object’s position compared to just measuring the distance traveled, as it shows the straight-line movement and direction.
Understanding Velocity
Velocity is the rate at which displacement changes over a specific interval of time. It is a vector quantity, meaning it has both magnitude and direction, unlike speed, which only considers the magnitude of movement. The SI unit of velocity is m/s⁻¹ or meters per second, and it represents how fast something moves in a specific direction, showing the rate of change in displacement over time. You can also read about local oscillator.
Average Velocity Explained
Average velocity is calculated by dividing the total displacement by the total time it takes for a moving body to travel from the initial point to the final point. It is an estimate of the velocity over a certain distance. The equation for average velocity is given as:
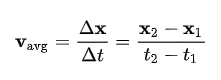
Here, x1 and x2 represent the positions at times t1 and t2, respectively. The magnitude of this velocity is also called the average speed. Mathematically, it helps us understand how fast something is moving over a period.
Instantaneous Velocity
Instantaneous velocity denotes the speed and direction of an object at a particular moment in time. It can be calculated by taking the limit of the average velocity as the time interval (Δt) approaches 0. Mathematically, it is given by the equation:
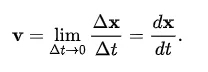
Here, Δx is the displacement, and dx and dt represent small changes in position and time, respectively. The magnitude of this velocity is called instantaneous speed, and it shows how fast the object is moving at a given moment.
Acceleration in Linear Motion
Acceleration is the rate at which velocity changes over time. It is defined as the change in velocity (Δv) divided by the time interval (Δt), or mathematically:
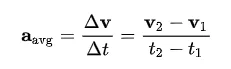
The SI unit of acceleration is m⋅s⁻². For instantaneous acceleration, we take the limit as the time interval (Δt) approaches zero, which gives us:
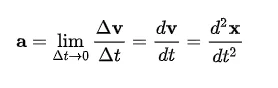
This shows how the position and velocity change over time, providing a clear picture of an object’s acceleration.
Equations of Motion
In linear motion, the relationship between acceleration, velocity, and displacement can be described by the equations of motion. For constant acceleration, we use the equation:
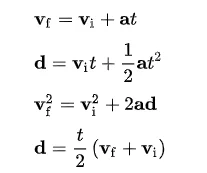
Where vi is the initial velocity, vf is the final velocity, a is the acceleration, and t is time.
The gradient of a velocity-time graph represents velocity, and the area under the graph gives the displacement. Similarly, the area under the acceleration-time graph shows the change in velocity.
Linear Motion vs. Rotation: Key Differences
In linear motion, we use terms like displacement (x), velocity (v), and acceleration (a) to describe an object’s movement. When we compare this to rotational motion, angular displacement (θ), angular velocity (ω), and angular acceleration (α) are used instead. The kinetic energy in linear motion is calculated as 1/2 mv², while in rotational motion, it is 1/2 Iω².
| Linear Motion | Rotational Motion |
|---|---|
| Displacement = x | Angular Displacement = θ |
| Velocity = v | Angular Velocity = ω |
| Acceleration = a | Angular Acceleration = α |
| Kinetic Energy = 1/2 mv² | Kinetic Energy = 1/2 Iω² |
The key difference is that rotational motion deals with rotational quantities, like moment of inertia (I) and angular momentum (L), which depend on the radius (r) and the mass (m) of the object. Similarly, force and torque are used to describe the forces acting on objects in both types of motion.
Conclusion
In conclusion, understanding linear motion is fundamental to grasping the basic principles of how objects move. From displacement and velocity to acceleration, these key concepts form the building blocks for analyzing motion in a straight line. By comparing linear motion to rotational motion, we gain deeper insights into the similarities and differences in how objects move in both scenarios. Whether it’s a simple or complex motion, these principles help us predict and understand the behavior of objects in the world around us.


